Von Neumann's inequality
In operator theory, von Neumann's inequality, due to John von Neumann, states that, for a contraction T acting on a Hilbert space and a polynomial p, then the norm of p(T) is bounded by the supremum of |p(z)| for z in the unit disk."[1] In other words, for a fixed contraction T, the polynomial functional calculus map is itself a contraction. The inequality can be proved by considering the unitary dilation of T, for which the inequality is obvious.
This inequality is a specific case of Matsaev's conjecture. That is that for any polynomial P and contraction T on 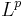
where S is the right-shift operator. The von Neumann inequality proves it true for 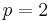 and for
and for 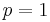 and
and 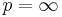 it is true by straightforward calculation. S.W. Drury has recently shown that the conjecture fails in the general case[2].
it is true by straightforward calculation. S.W. Drury has recently shown that the conjecture fails in the general case[2].